Arne soll sein Zimmer aufräumen. Er möchte all seine Brettspiele in eine Box legen. Dazu hat er zwei Boxen zur Auswahl:
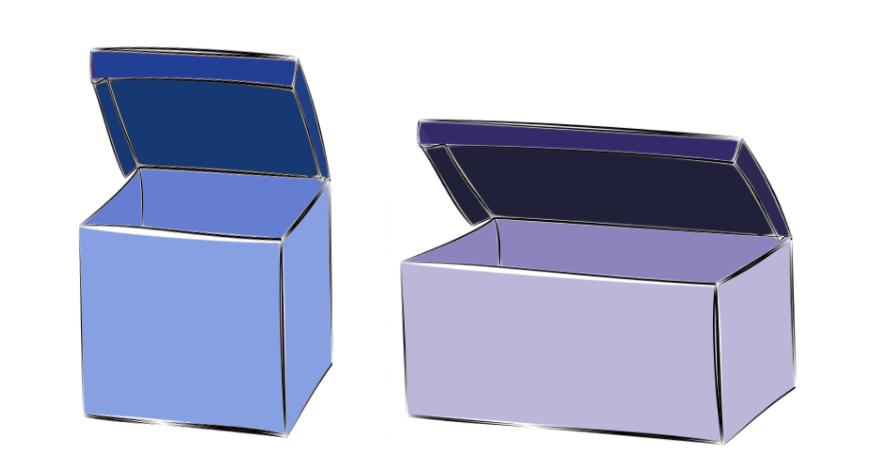
Arne möchte die linke Box nehmen, die ist nämlich größer, behauptet er.
Seine Schwester ist immer anderer Meinung. Sie behauptet die rechte Box sei größer.
Wer hat denn nun recht?
1. Möglichkeit:
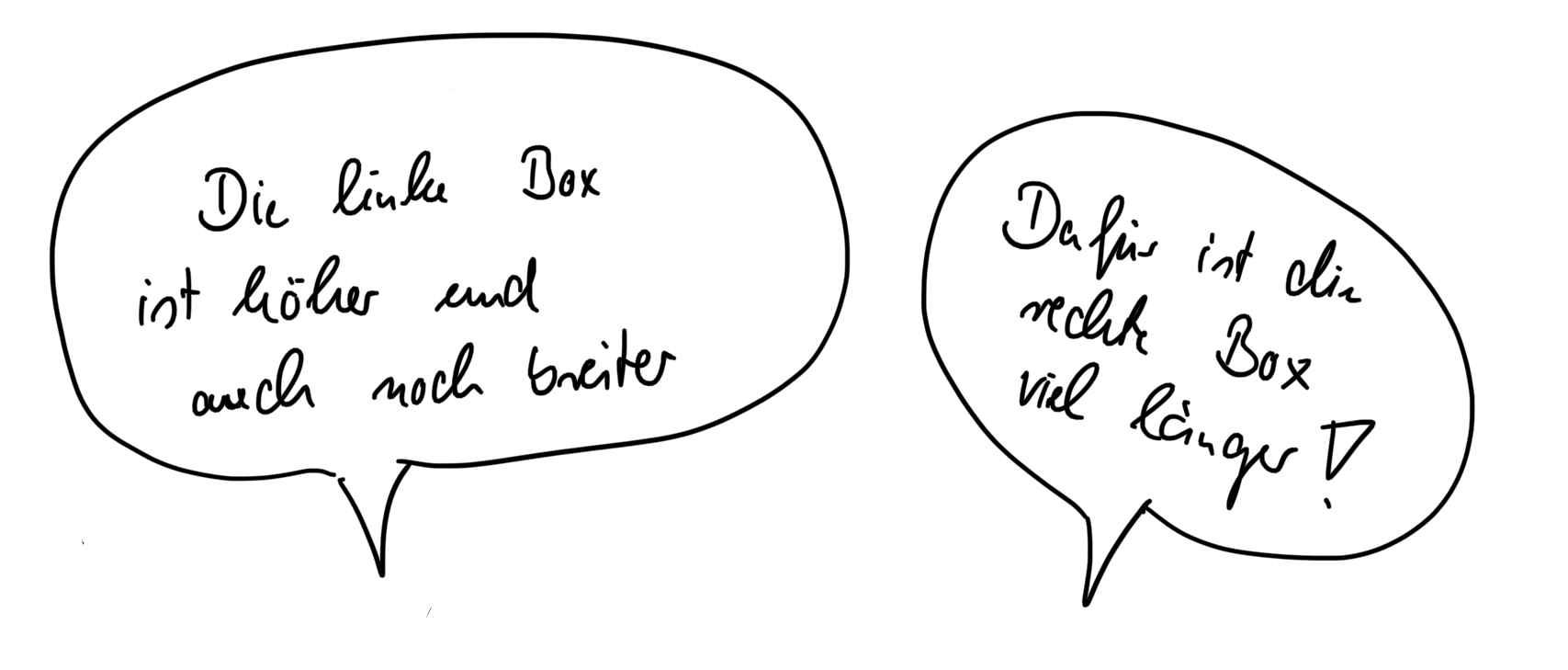
Die Geschwister sind sich immer noch nicht einig, deshalb suchen sie nach einer anderen Methode, um entscheiden zu können, welche Box größer ist.
2. Möglichkeit:
Die Boxen sollen genutzt werden, um Brettspiele aufzubewahren. Die größere Box sollte also die sein, in der am meisten solche Spiele reinpassen. Daher füllen beide nacheinander ihre Boxen mit den gleichen Brettspielen und zählen dann wie viele reinpassen.
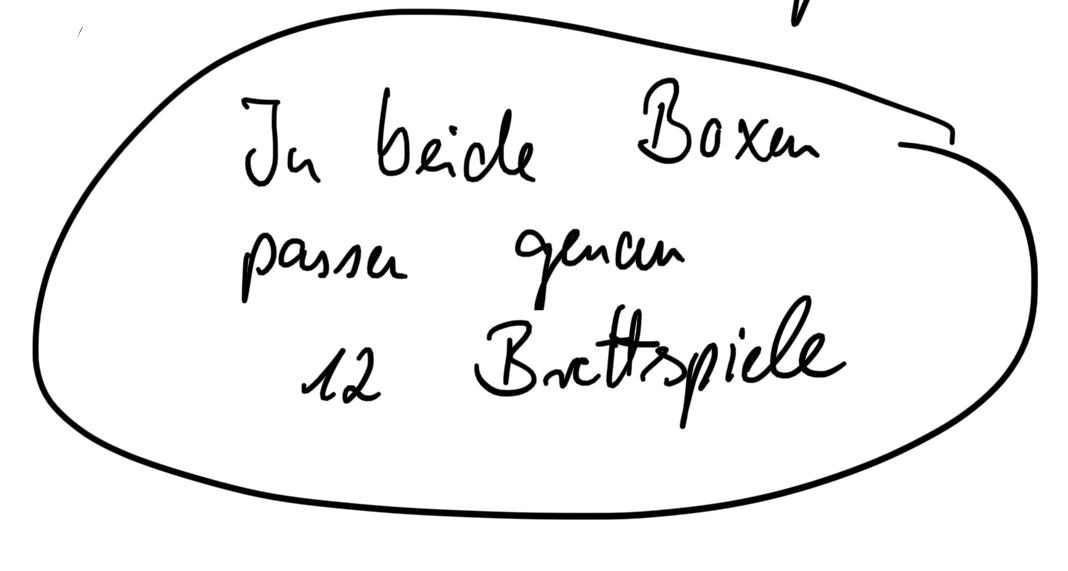
3. Möglichkeit: Einheitswürfel
Ein Würfel der Kantenlänge 1 Längeneinheit (kurz: 1 LE) wird als Einheitswürfel bezeichnet. Dabei kann LE dir bekannte Längeneinheiten sein: mm, cm, dm, m.
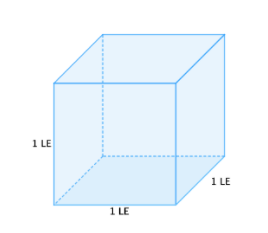
Merkhefteintrag:

Wie geht das nun mit den Einheitswürfeln?
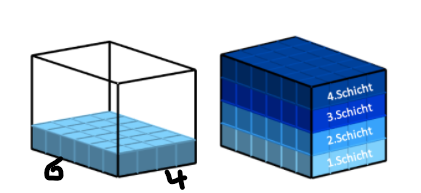
Ihr habt einen Quader, in dem ihr am Boden mit Einheitswürfel mit 1 cm Kantenlänge auslegt – vollständig und ohne Lücke:
6 mal 4 Einheitswürfel = 24 Einheitswürfel
Damit der Quader voll wird, benötigt ihr 4 solcher Schichten. Also:
24 Einheitswürfel mal 4 Schichten = 96 Einheitswürfel.
Ein Einheitswürfel hat 1 cm³ Rauminhalt, also hat der Quader insgesamt 96 mal 1 cm³ Rauminhalt = 96 cm³ Volumen.