Eine Pyramide wird von einem Vieleck, der sogenannten Grundfläche, und von Dreiecken begrenzt, die alle einen Punkt, die Spitze der Pyramide, gemeinsam haben.
Hat eine Pyramide ein Dreieck (Viereck, Fünfeck, …) als Grundfläche, dann hat sie drei (vier, fünf, …) Seitenflächen. Deshalb wird sie auch als dreiseitige (vierseitige, fünfseitige, …) Pyramide bezeichnet.
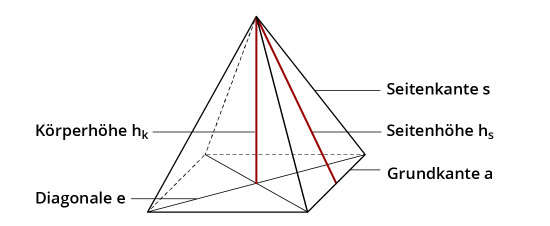Der Abstand der Spitze der Pyramdie von der Grundfläche ist die Höhe der Pyramide.
Alle Seitenkanten gehen durch die Spitze.
Eine Pyramide, deren Grundfläche ein regelmäßiges Vieleck (gleichseitiges Dreieck, Quadrat, regelmäßiges Fünfeck, …) ist und deren Seitenkanten gleich lang sind, nennt man gerade regelmäßige Pyramide.
Netz und Oberfläche
Wie ein Netz entsteht und wie die Oberfläche einer quadratischen Pyramide berechnet wird, siehst du hier:
Für die Oberfläche O einer Pyramide mit der Grundfläche G und der Mantelfläche M gilt:
Oberfläche = Grundfläche + Mantel
O = G + M
Volumen
Für das Volumen V einer Pyramide gilt:
V = ⅓ · G · h
Herleitung:
Füllst du die Pyramide mit einer Flüssigkeit und schüttest diese anschließend in den Quader, so ist dieser zu einem Drittel gefüllt.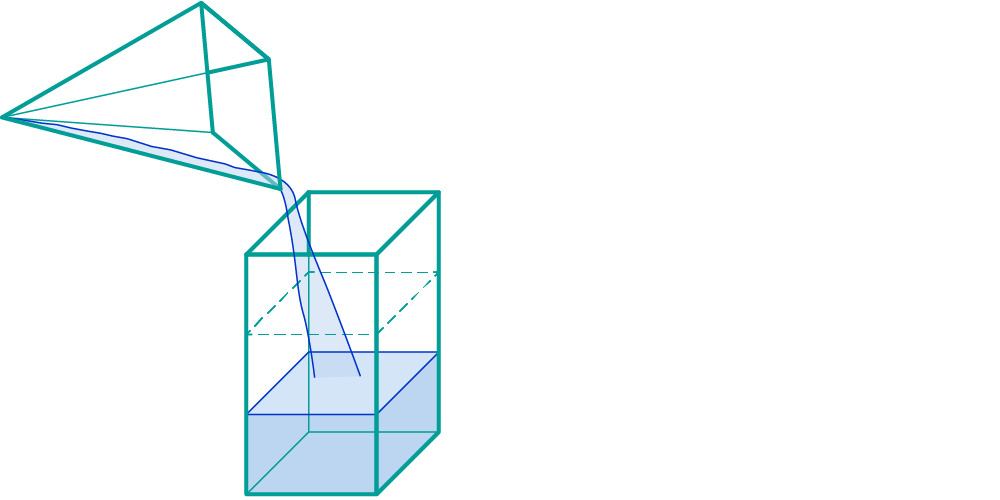 
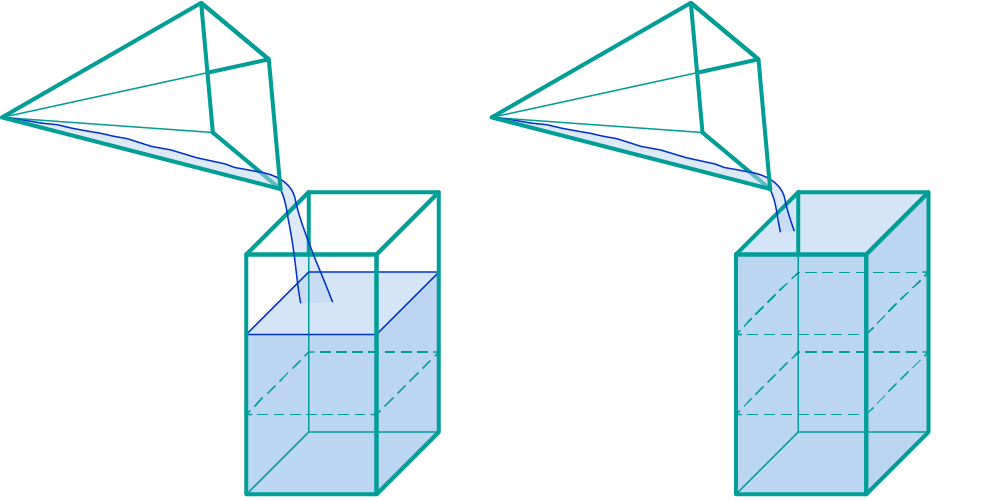
Wiederholst du diesen Vorgang noch zweimal, ist der Quader voll.
Das Volumen des Quaders ist demnach dreimal so groß wie das Volumen der Pyramide. oder Die Pyramide passt dreimal in den Quader.
Aufgaben
S. 111/4 – S.111 /5