Ein Zylinder, dessen Grundfläche eine Kreisfläche ist, nennt man Kreiszylinder.
Der Mantel eines Zylinders ist ein Rechteck.
Durch Drehung eines Rechtecks entsteht ein Zylinder. Wegen dieser Erzeugungsart nennt men den entstehenden Körper
auch Drehkörper (Rotationskörper). Deshalb bezeichnet man einen geraden Kreiszylinder auch als Drehzylinder.
Die Gerade, um die die Drehung erfolgt, heißt Drehachse des Drehzylinders.
Netz und Oberfläche
Wenn du den Zylinder zu einem Netz ausklappt, kannst du alle äußeren Flächen gut erkennen:
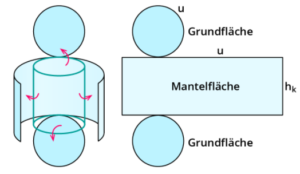
Du siehst die Mantelfläche und zweimal die Grundfläche. Man nennt diese äußeren Flächen des Zylinders seine Oberfläche.
Wenn du das Netz eines Zylinders zeichnest, ist es am übersichtlichsten, wenn du die Grundflächen oben und unten von der Mantelfläche zeichnest. Alle Flächen behalten dabei ihre Originalgröße. Die Mantelfläche hat die Seitenlängen: Umfang u des Kreises sowie die Körperhöhe hk.
M = 2 · r · π · h.
So berechnest du den Oberflächeninhalt eines Zylinders:
O = 2 · G + M
O = 2 · r2 · π + 2 · r · π · h
O = 2 · r · π · (r+h)
Volumen
Einen Drehzylinder kann man als Grenzfall eines regelmäßigen Prismas mit einer sehr großen Anzahl von Ecken auffassen.
Daraus ergibt sich für das Volumen eines Drehzylinders:
V = G · H
V = Grundlfäche · Höhe
V = r2 · π · h
Aufgaben
S. 116/3 – 116/5